M.M.C e M.D.C. como fazê-los.

 Mínimo Múltiplo Comum, reduzido fica MMC, e serve para indicar o menor múltiplo de um número ou mais de um número,múltiplo é simplesmente o número de é divisivel por outro. como por exemplo o número 24 que é divisivel por 3 , então dizemos que ele é múltiplo de 3 

Os múltiplos de um número são calculados multiplicando-se esse número pelos números naturais.

        Exemplo: os múltiplos de 7 são:
                            7x0 , 7x1, 7x2 , 7x3 , 7x4 , ...  = 0, 7, 14, 21, 28,... e aí vai...

duas coisas que você tem que notar é que o zero é múltiplo de qualquer número natural, e também todo número tem infinitos múltiplos.

  Para calcular o mmc de dois ou mais números devemos ultilizar a fatoração, aqui iremos calcular o mmc de 12 e 30. 

    1º) decompomos os números em fatores primos
    2º) o m.m.c. é o produto dos fatores primos comuns e não-comuns:

                   12   =  2  x  2  x  3
                   30   =          2  x  3   x  5
        m.m.c (12,30)  = 2  x  2  x  3   x  5

        Escrevendo a fatoração dos números na forma de potência, temos:
        12 = 2²  x  3
        30 = 2   x  3  x  5
        m.m.c (12,30)  = 2²  x  3  x  5

O mmc de dois ou mais números, quando fatorados é o produto dos fatores comum e não comuns a eles, cada um elevado ao maior expoente.

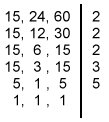
   Processo de decomposição simuntânea.

 Nesse tipo de Processo que além do mais é o mais comum, decompomos todos os números no mesmo tempo.

 Exemplo:

 

Lembrando que só dividimos por números primos.

O produto dos fatores primos que conseguimos nessa decomposição é o mmc desses três números 

Portanto, m.m.c.(15,24,60) = 2 x 2 x 2 x 3 x 5 = 120. 

Espero que tenha entendido.

MDC 

 Dois números naturais sempre têm divisores comuns. Por exemplo: os divisores comuns de 12 e 18 são 1,2,3 e 6. Dentre eles, 6 é o maior. Então chamamos o 6 de máximo divisor comum de 12 e 18 e indicamos m.d.c.(12,18) = 6.

mdc (6,12) = 6
         mdc (12,20) = 4
         mdc (20,24) = 4
         mdc (12,20,24) = 4
         mdc (6,12,15) = 3

  

 Um modo de calcular o m.d.c. de dois ou mais números é utilizar a decomposição desses números em fatores primos.

 decompomos os números em fatores primos;
  o m.d.c. é o produto dos fatores primos comuns.

Acompanhe o cálculo do m.d.c. entre 36 e 90:
36 = 2 x 2 x 3 x 3
90 =       2 x 3 x 3 x 5

O m.d.c. é o produto dos fatores primos comuns =>   m.d.c.(36,90) = 2 x 3 x 3
Portanto m.d.c.(36,90) = 18.

Escrevendo a fatoração do número na forma de potência temos:
36 = 2² x 3²
90 = 2  x 3² x5
Portanto m.d.c.(36,90) = 2 x 3² = 18.

Esse vídeo pode colaborar com seu aprendizado.

"tudo que pedirdes em oração crendo recebereis"

Frações

 Adição e subtração de números fracionários 

Para podermos fazer a adição de frações temos que observar primeiro dois casos, um mais simples e outro que exige um pouco mais de você.

 O primeiro caso é de frações que tem o denominador igual.  Lembrando, denominador é a parte de baixo da fração e a parte de cima chamamos de numerador.

  Para somar frações com denominadores iguais, basta somar os numeradores e conservar o denominador, o mesmo acontece na subtração.                          

 :

  

 Jà quando a fração tem denominadores diferentes uma solução é obter frações equivalentes, de denominadores iguais ao MMC dos dois denominadores.

vamos somar as frações   Exemplo: somar as frações .

        Obtendo o MMC dos denominadores temos MMC de 5 e 2 = 10

(10:5).4 = 8

(10:2).5 = 25

       

        Resumindo: utilizamos o MMC para obter as frações equivalentes e depois somamos normalmente as frações, que já terão o mesmo denominador.

 Multiplicação e divisão de frações 

   Na multiplicação de números fracionários, devemos multiplicar numerador por numerador, e denominador por denominador, assim como é mostrado nos exemplos abaixo:

   

    Na divisão de números fracionários, devemos multiplicar a primeira fração pelo inverso da segunda, como é mostrado no exemplo abaixo:

   

 

   

 e finalmente potenciação e radicação das frações.

  Na potenciação, quando elevamos um número fracionário a um determinado expoente, estamos elevando o numerador e o denominador a esse expoente, conforme  os exemplos abaixo: 

  Na radiciação, quando aplicamos a raiz quadrada a um número fracionário, estamos aplicando essa raiz ao numerador e ao denominador, conforme o exemplo abaixo:

   

Esses vídeos também pode ajudar você 

Matemática Zero canal do YouTube, 

Matemática Zero - Aula 8 - Frações - primeira Parte

Matemática Zero - Aula 8 - Frações - Segunda Parte

Matemática Zero - Aula 8 - Frações - Terceira Parte - Final

 Espero que esses vídeos ajudem você. 

Estudo das razões em matemática

  A comparação entre dois números racionais, através de uma divisão, chama-se razão.
 vamos entender melhor sobre razões nessa postagem
  
  Vamos considerar dois edifícios, um têm  35 metros de altura e o outro tem 70 metros de altura, a razão entre a altura desses dois edificios é de 35:70 

ou seja um meio, podemos dizer então que o segundo edifício tem o dobro de altura do primeiro.  chamos de razão o quociente ou seja o resultado da divisão entres dois números "a" e "b" sendo "b" diferente de zero.  
       
    o quociente ou a:b.    

 Outro exemplo que uma professora do meu curso de auxiliar administrativo deu.

A palavra razão, vem do latim ratio, e significa "divisão". Como no exemplo anterior, são diversas as situações em que utilizamos o conceito de razão. Exemplos: 

 Dos 1200 inscritos num concurso, passaram 240 candidatos.
Razão dos candidatos aprovados nesse concurso:

              (de cada 5 candidatos inscritos, 1 foi aprovado).  

A razão entre dois números racionais pode ser apresentada de três formas. Exemplo:
            Razão entre 1 e 4:     1:4   ou    ou 0,25.

Esse vídeo também pode ajudar você 

Vamos aprender?

 Criei o blog  "link matemático" com o objetivo de compartlhar meus conhecimentos e aprender muito mais com meus visitates, vejo esse blog como uma oportunidade de aprendizado, e nada mais justo do que compartilhar todo esse conhecimento com vocês leitores, sou um garoto de apenas 15 anos me chamo Murilo Santos e espero colaborar com seu saber.
   tudo o que publicarei aqui será editado antes no meu caderno de anotações para que vocês tenham um conteúdo único e que não seja uma poluição a internet.
  Nas postagens mostraremos passo-a-passo regra por regra como fazer no papel cada conceito matemático. tenho determinados assuntos que serão mostrads em lista, se você quiser outros assuntos faça um comentário com seu pedido.


  Lista de assuntos que possívelmente serão abordados aqui :

Ensino Fundamental 

Frações
Máximo Divisor Comum
Mínimo Múltiplo Comum 
Equações do primeiro grau
Inequações do primeiro grau (Em breve)
Radiciação

Razões
Proporções
Algarismos Romanos
Grandezas Proporcionais
Dízimas periódicas
Porcentagem
Polígonos
Equações do segundo grau (Em breve)
Números decimais 



" Existe apenas duas coisas que nunca voltam, a flexa lançada e aportunidade perdida"
                                              Autor Desconhecido

   " O único lugar onde sucesso vem antes de trabalho é no dicionário"


 Futuramente teremos videos em todas as postagens. e um canal no youtube.
ML+ Produções 2013