Esta postagem é dedicada ao aprimoramento dos estudos sobre Equações do Primeiro Grau.
Uma equação do 1° Grau é toda sentença matemática que tem base na fórmula ax+b=0, são sempre duas expressões que apresentam igualdade em seus valores.
ax+b=0 o que isso quer dizer?
simples a letra "a" e a letra "b" podem ser qualquer número, e a letrinha "x" e o valor que vc tem que descobrir.
 |
| Na maioria das equações teremos que procurar o valor desse carinha aí o "x" mais também poderão aparecer outras letras. |
veja o exemplo:
12x+6=0
nesse caso aqui o "a" é o número 12 e o "b" e o número 6, o "a" representa a quantidade de "xises".
mais o ultimo número não precisa ser sempre "0" pode ser de outras formas também, além disso pode ser qualquer umas das operações fundamentais, frações, potências e por aí vai.
exemplo:
60-x+12=3x+1
COMO INTERPRETAR UMA EQUAÇÃO POR UMA PERGUNTA?
exemplo: x+8=15 " Qual o número que somado a 8 tem resultado 15" é só usar sua imaginação.
COMO RESOLVER DIVERSOS TIPOS DE EQUAÇÕES
Quando se tem uma equação com adição e subtração a regra é simples "Adicionando um mesmo número a ambos os membros de uma equação, ou subtraindo um mesmo número de ambos
os membros, a igualdade se mantém."
Exemplo: 60-x+12=3x+1
primeiro separamos termos iguais no caso "x" e os números naturais 60,12 e 1.
um de um lado e outro do outro, mais lembre-se "troque o sinal"
veja: -x-3x=-60-12+1
depois resolvas as operações. lembre-se -x = -1x e x e = a 1x , só que o 1 não é obrigado aparecer.
veja: -x-3x=-60-12+1
-4x= -60 -12+1
-4x=-72 +1
-4x=-71
x= -71:-4
Pronto!.
-4x=-72 +1
-4x=-71
x= -71:-4
Pronto!.
Agora vamos resolver uma com multiplicação e divisão.
Agora para resolver uma equação que contém multiplicação e divisão é só pensarmos que uma é o inverso da outra. A multiplicação é o inverso da divisão e vice-versa.








 lados (
lados (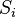 ) é dada por
) é dada por 
 ) é igual a
) é igual a 
 ) é dada por
) é dada por
 ) é dada por
) é dada por
 ) é igual a
) é igual a 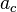 ) é dada por
) é dada por
 diagonais (
diagonais ( ).
). ) de um polígono é dado por
) de um polígono é dado por  onde
onde 


 equivale à fração
equivale à fração  que equivale ao número decimal
que equivale ao número decimal 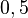 .
.



.jpg)


